Пятиугольник со всеми диагоналями - это многоугольник, который имеет пять вершин и все возможные диагонали, соединяющие эти вершины. Каждая диагональ пятиугольника создает новый треугольник, а также принадлежит очередному треугольнику, который образуется после соединения двух диагоналей. Интересно узнать, сколько треугольников можно образовать внутри пятиугольника со всеми диагоналями.
Для вычисления общего количества треугольников в пятиугольнике со всеми диагоналями, мы можем использовать формулу, известную как "формула треугольника". Согласно этой формуле, для пятиугольника со всеми диагоналями, содержащим n вершин, общее количество треугольников равно (n-2)(n-3)/2.
Применяя эту формулу к пятиугольнику, мы получаем (5-2)(5-3)/2 = 3. Таким образом, пятиугольник со всеми диагоналями содержит три треугольника. Это значит, что мы можем найти три треугольника, образованных треугольниками, внутри пятиугольника, которые имеют общие стороны с диагоналями.
Количество треугольников в пятиугольнике
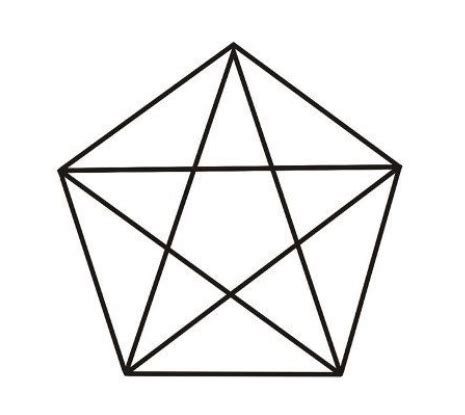
Количество треугольников = (n * (n - 1) * (n - 2)) / 6,
где n - количество вершин пятиугольника.
Заметим, что в пятиугольнике каждая вершина соединена с четырьмя другими вершинами (все вершины, кроме двух соседних). Поэтому, если мы возьмем любую вершину пятиугольника, то у нее будет четыре соседних вершины, с которыми она может образовать треугольник. Таким образом, для каждой вершины пятиугольника имеется 4 возможных варианта соединения с другими вершинами.
Учитывая, что в пятиугольнике всего пять вершин, получаем, что количество треугольников равно:
(5 * 4 * 3) / 6 = 10.
Таким образом, в пятиугольнике со всеми диагоналями имеется 10 треугольников.
Раздел 1: Размещение диагоналей в пятиугольнике
В пятиугольнике каждая сторона соединяется с каждой другой стороной, образуя диагонали. Количество диагоналей зависит от количества сторон и может быть рассчитано с использованием формулы:
Количеств
Способы размещения диагоналей
Для пятиугольника существует несколько способов размещения диагоналей, которые позволяют нам определить количество треугольников, образованных этими диагоналями. Рассмотрим некоторые из них.
Способ Количество треугольников Размещение одной диагонали 0 Размещение двух диагоналей 0 Размещение трех диагоналей 0 Размещение четырех диагоналей 5 Размещение пяти диагоналей 5 Как видно из таблицы, наибольшее количество треугольников (5) образуется при размещении четырех или всех пяти диагоналей. При размещении одной, двух или трех диагоналей треугольники не образуются.
Таким образом, чтобы найти количество треугольников в пятиугольнике со всеми диагоналями, нужно либо разместить четыре, либо все пять диагоналей.
Раздел 2: Формула для подсчета количества треугольников
Найдем формулу, позволяющую подсчитать количество треугольников в пятиугольнике со всеми диагоналями.
При подсчете треугольников в пятиугольнике необходимо учесть, что для каждой вершины выбирается еще две вершины. Таким образом, каждая вершина участвует в образовании двух треугольников . У нас есть пять вершин в пятиугольнике, поэтому общее количество треугольников без учета пересечений будет равно 5 * 2 = 10 .
Однако, в результате, некоторые треугольники пересекаются. Чтобы учесть это, нужно вычесть количество пересечений из общего числа треугольников.
Создадим таблицу, в которой каждой диагонали будет соответствовать номер:
Диагональ Номер AD 1 BD 2 CD 3 DE 4 AE 5 BE 6 CE 7 Воспользуемся формулой: Общее количество треугольников = 10 - количество пересечений .
Чтобы найти количество пересечений, зафиксируем одну вершину пятиугольника, например, вершину A. Подсчитаем количество возможных сочетаний из двух вершин, не являющихся соседними для вершины A.
Следовательно, количество пересечений составляет 3 * 2 = 6 (три возможных сочетания для вершины A, умноженное на два треугольника для каждого сочетания).
Подставим полученное значение в формулу и получим: Общее количество треугольников = 10 - 6 = 4 .
Таким образом, в пятиугольнике со всеми диагоналями можно образовать 4 треугольника .
Расчет количества треугольников
Для расчета количества треугольников в пятиугольнике со всеми диагоналями, мы можем использовать сочетания и комбинаторику.
Каждый треугольник в пятиугольнике образуется тремя вершинами из пяти возможных. Давайте проведем таблицу и посчитаем количество треугольников для каждой комбинации вершин.
Вершина A Вершина B Вершина C Количество треугольников 1 2 3 1 1 2 4 2 1 2 5 3 1 3 4 4 1 3 5 5 1 4 5 6 2 3 4 7 2 3 5 8 2 4 5 9 3 4 5 10 Итак, получается, что в пятиугольнике со всеми диагоналями находится 10 треугольников.
Раздел 3: Пример подсчета количества треугольников
Для наглядного примера подсчета количества треугольников в пятиугольнике со всеми диагоналями, рассмотрим следующую ситуацию:
Предположим, у нас есть пятиугольник ABCDE с вершинами A, B, C, D и E. Мы хотим выяснить, сколько треугольников можно образовать, используя эти вершины и соединяя их диагоналями.
Для начала, посмотрим на отдельные треугольники, образованные каждой вершиной в качестве вершины треугольника:
Треугольники, в которых A является вершиной:
ABD, ACD, ADE, ABE
Треугольники, в которых B является вершиной:
ABC, ABD, ABE, BCE
Треугольники, в которых C является вершиной:
ABC, ACD, BCE, CDE
Треугольники, в которых D является вершиной:
ABD, ACD, ADE, CDE
Треугольники, в которых E является вершиной:
ADE, ABE, BCE, CDE
Далее, рассмотрим треугольники, образованные двумя вершинами и одной диагональю:
Треугольники, образованные диагоналями AB, AC и AD:
ABC, ABD, ACD
Треугольники, образованные диагоналями BC, BD и BE:
ABC, BCE, ABE
Треугольники, образованные диагоналями CD, CE и DE:
ACD, BCE, CDE
Треугольники, образованные диагоналями DE, DA и DB:
ADE, ABE, CDE
Треугольники, образованные диагоналями EA, EB и EC:
ADE, ABE, BCE
Таким образом, общее количество треугольников, образованных вершинами пятиугольника ABCDE и его диагоналями, равно 20.