В математике существует множество способов провести плоскости через две точки, и это представляет большой интерес для исследователей и студентов в области геометрии. Количество плоскостей, которые можно провести через две заданные точки, зависит от их положения и расстояния друг от друга.
Для начала, давайте разберемся с терминами. Плоскость - это двумерная геометрическая фигура, которая состоит из бесконечного множества точек и распространяется во все направления. Точка - это объект, который не имеет никаких размеров и описывается только своими координатами.
Теперь давайте рассмотрим простой пример. Представьте, что у нас есть две точки A и B в трехмерном пространстве. Сколько плоскостей можно провести через эти две точки? Ответ - бесконечно много! Потому что для определения плоскости нам необходимо иметь еще одну точку, а возможных точек в бесконечном пространстве бесконечно много.
Однако, если мы ограничимся определенной областью пространства или будем искать плоскости, которые проходят через две заданные точки A и B, но также должны пересекать направляющие векторы AB, то возможных вариантов будет конечное число. Это связано с тем, что плоскость, которая проходит через две точки и пересекает направляющие векторы AB, однозначно определяется.
Количество плоскостей через две точки

Для определения количества плоскостей, проходящих через две заданные точки, необходимо учесть следующие факты:
1. Плоскость определяется тремя неколлинеарными точками. Таким образом, чтобы определить плоскость, проходящую через две точки, необходимо задать третью точку, которая не лежит на прямой, проходящей через эти две точки.
2. Чтобы определить третью точку, можно использовать различные подходы. Например, можно выбрать точку, лежащую на плоскости, проходящей через данные две точки и перпендикулярной заданной плоскости. Или можно выбрать точку, лежащую на прямой, параллельной заданной плоскости и проходящей через одну из заданных точек.
3. После выбора третьей точки, можем построить плоскость, проходящую через заданные две точки, используя метод построения, например, с использованием векторов или нормали к плоскости.
4. Таким образом, количество плоскостей, проходящих через две заданные точки, может быть бесконечным, так как третью точку можно выбрать бесконечное количество способов.
Для лучшего понимания данной концепции, можно рассмотреть примеры и иллюстрации в таблице ниже:
| Первая точка | Вторая точка | Третья точка | Полученная плоскость |
|---|---|---|---|
| (1, 2, 3) | (4, 5, 6) | (7, 8, 9) | // Иллюстрация плоскости |
| (0, 0, 0) | (1, 1, 1) | (2, 2, 2) | // Иллюстрация плоскости |
Таким образом, количество плоскостей, проходящих через две точки, не является конкретным числом и зависит от выбранной третьей точки.
Определение плоскости и количество плоскостей
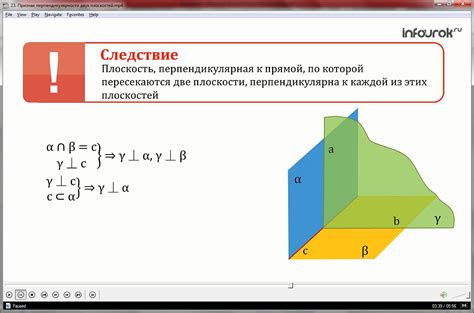
Одну плоскость можно определить с помощью трех несовпадающих точек, либо двух параллельных прямых. Если известно, что эти точки или прямые не являются коллинеарными, то они определяют единственную плоскость.
Количество плоскостей, которые могут быть проведены через две точки, зависит от того, находятся ли эти точки на одной прямой или нет.
Если две точки лежат на одной прямой, то через них можно провести бесконечно много плоскостей. В этом случае, плоскости могут быть сдвинуты вдоль прямой с сохранением положения двух точек на ней.
Если две точки не лежат на одной прямой, то через них можно провести только одну плоскость. Эта плоскость будет проходить через обе точки и будет перпендикулярна прямой, соединяющей эти точки.
Таким образом, определение плоскости и количество плоскостей, которые могут быть проведены через две точки, зависит от их взаимного расположения в пространстве.
Связь между двумя точками и плоскостью
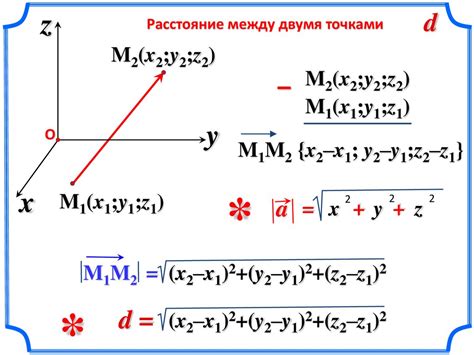
В геометрии существует тесная связь между двумя точками и плоскостью. Для определения плоскости, проходящей через две точки, необходимо учитывать их координаты в трехмерном пространстве.
Из двух точек можно построить множество плоскостей, но самое интересное заключается в том, что существуют бесконечное количество плоскостей, проходящих через эти две точки.
Для определения одной из возможных плоскостей, проходящих через две точки, можно использовать следующую формулу:
А(x - x1) + В(y - y1) + С(z - z1) = 0,
где (x1, y1, z1) и (x, y, z) – координаты двух точек.
Эта формула представляет собой уравнение плоскости в пространстве и прекрасно иллюстрирует связь между двумя точками и плоскостью.
Объяснение количества плоскостей
Чтобы понять, сколько плоскостей можно провести через две данной точки, необходимо учитывать особенности геометрической конструкции.
Если заданы две точки в трехмерном пространстве, то существует бесконечное количество плоскостей, проходящих через данные точки. Каждая из этих плоскостей можно представить как бесконечно много точек, лежащих на этой плоскости. При этом, плоскость определяется любой третьей точкой, лежащей не на прямой, соединяющей две заданные точки.
Если заданы две точки в плоскости, то через них можно провести бесконечное количество плоскостей. Плоскость в данном случае можно представить как бесконечное количество прямых, проходящих через данные точки. Каждая прямая можно определить, например, как линию, параллельную некоторой фиксированной прямой и проходящую через одну из заданных точек.
Другими словами, количество плоскостей, проходящих через две точки, зависит от размерности пространства и точного определения понятия "плоскость". В трехмерном пространстве можно провести бесконечное количество плоскостей через две данной точки, в то время как в плоскости можно провести бесконечное количество прямых через две данные точки.