Понимание того, сколько общих точек может быть у двух разных плоскостей, является важным аспектом в геометрии и математике. Общие точки определяют, насколько две плоскости пересекаются или пересекаются ли вообще. Подсчет общих точек важен для проведения анализа, решения задач и понимания взаимоотношений между плоскостями.
Определить количество общих точек у двух плоскостей можно с помощью различных методов. Один из самых простых методов, который используется в школьном курсе геометрии, основан на решении системы уравнений плоскостей. Путем решения системы можно найти точки пересечения плоскостей и определить их количество. Этот метод подходит для плоскостей в трехмерном пространстве.
Другой метод подсчета общих точек двух плоскостей основан на векторном анализе. Векторы нормалей к плоскостям помогают определить угол между ними и их совместную прямую. Если угол между нормалями равен нулю, то плоскости совпадают и имеют бесконечное количество общих точек. Если же угол между нормалями равен 90 градусам, то плоскости параллельны и не имеют общих точек. Во всех остальных случаях плоскости пересекаются и имеют одну общую точку или образуют прямую, которая пересекает обе плоскости.
Сколько общих точек у двух разных плоскостей

Если у нас есть две разные плоскости, то возникает вопрос – сколько у них общих точек? Ответ на этот вопрос зависит от взаимного расположения плоскостей в пространстве.
Одним из методов подсчета общих точек двух плоскостей является использование системы уравнений. Если у нас есть уравнения для каждой плоскости в виде Ax + By + Cz + D = 0, то можно составить систему из двух уравнений и найти их общее решение. Это будет координаты точки, которая принадлежит обоим плоскостям.
Другой метод заключается в определении прямой, пересекающей обе плоскости. Если такая прямая существует, то она будет иметь бесконечно много точек пересечения с каждой из плоскостей.
Также существуют специальные случаи, когда две плоскости могут быть параллельными или совпадающими. В этом случае они будут иметь либо ноль общих точек, либо бесконечно много общих точек.
Важно отметить, что количество общих точек у двух плоскостей может варьироваться в зависимости от их расположения и характеристик. Наиболее точный и надежный способ определить это – использование вышеупомянутых методов.
| Случай | Количество общих точек |
|---|---|
| Две пересекающиеся плоскости | Одна (точка) |
| Две параллельные плоскости | Ни одной (0) |
| Две совпадающие плоскости | Бесконечно много |
Таким образом, ответ на вопрос о количестве общих точек двух разных плоскостей зависит от их взаимного расположения. Существуют различные методы подсчета, которые могут быть применены для определения этого числа.
Определение понятия "общие точки плоскостей"
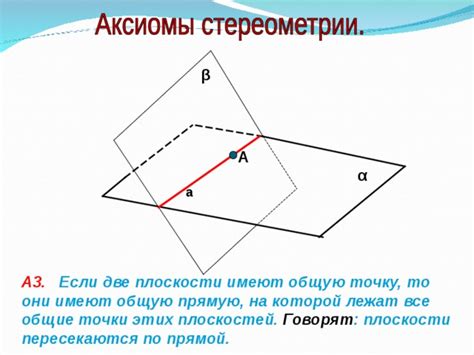
Общие точки плоскостей могут иметь различные свойства и характеристики. Например, они могут образовывать линию, когда пересекаются только две плоскости, или же могут образовывать плоскость, когда пересекаются три или более плоскостей.
Для определения количества общих точек двух разных плоскостей необходимо рассмотреть их параметры и уравнения. В зависимости от вида уравнений плоскостей существуют различные методы и алгоритмы для подсчета общих точек.
Определение общих точек плоскостей имеет широкое применение в различных областях науки и техники, таких как компьютерная графика, аэронавтика, архитектура и другие. Понимание этого понятия позволяет проводить анализ и решать задачи, связанные с взаимодействием плоскостей в трехмерном пространстве.
Методы подсчета общих точек плоскостей
В математике существует несколько методов для подсчета общих точек двух разных плоскостей. Рассмотрим некоторые из них:
1. Системы уравнений: один из самых распространенных методов. Для этого нужно записать уравнения каждой плоскости в виде системы линейных уравнений. Затем решить систему и найти значения переменных, которые будут определять общие точки плоскостей.
2. Векторное произведение: этот метод основан на свойствах векторного произведения двух ненулевых векторов. Если векторное произведение двух нормалей плоскостей не равно нулю, то плоскости пересекаются в одной прямой. Если векторное произведение равно нулю, то плоскости могут быть параллельными или совпадающими.
3. Линии пересечения: данный метод используется, когда две плоскости параллельны или совпадают. В этом случае можно найти линию пересечения, которая будет содержать бесконечное количество общих точек.
4. Геометрический метод: в данном методе используется геометрическая интерпретация плоскостей и их взаимного расположения в трехмерном пространстве. Подсчет общих точек осуществляется на основе визуализации и анализа графического представления плоскостей.
Выбор метода зависит от характера плоскостей и конкретной задачи. Возможно использование комбинации разных методов для получения наиболее точного результата подсчета общих точек плоскостей.
Метод 1: Графический способ
Для начала, следует определить уравнения заданных плоскостей. Уравнение плоскости обычно задается в виде Ax + By + Cz = D, где A, B, C, D - коэффициенты, характеризующие плоскость.
Далее, используя полученные уравнения, можно построить графики соответствующих плоскостей на координатной плоскости. Пометив точки пересечения плоскостей на графике, можно легко определить их количество.
Если точек пересечения нет, то это означает, что две плоскости параллельны друг другу и не имеют общих точек. Если же количество точек пересечения равно 1, то плоскости пересекаются по одной прямой, и так далее.
Примечание: Графический способ подходит для рассмотрения плоскостей в двумерном пространстве, а также при условии, что уравнения плоскостей несложные и их графики легко построить.
Метод 2: Аналитический способ

Аналитический способ нахождения общих точек двух разных плоскостей позволяет решить данную задачу с использованием алгебраических методов. Он основан на исследовании уравнений плоскостей и их систем.
- Прежде всего, необходимо записать уравнения двух плоскостей в общем виде. Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C - коэффициенты при переменных, а D - свободный член.
- Составим систему уравнений, включающую уравнения обоих плоскостей. Для этого вычислим коэффициенты A, B, C и D для каждой плоскости и объединим их уравнения в систему.
- Решим систему уравнений методом Гаусса или любым другим алгоритмом решения систем линейных уравнений. Полученные значения переменных будут координатами общей точки плоскостей.
Таким образом, применение аналитического способа позволяет точно определить общие точки двух разных плоскостей, используя алгебраические методы решения систем линейных уравнений.
Метод 3: Геометрический способ

Геометрический способ подсчета числа общих точек у двух разных плоскостей основан на рассмотрении их взаимного расположения в трехмерном пространстве. Для этого метода нам понадобится определить уравнение каждой плоскости и найти их пересечение.
Возьмем две плоскости P1 и P2. Каждая плоскость может быть представлена в виде уравнения вида:
A1x + B1y + C1z + D1 = 0 для плоскости P1
A2x + B2y + C2z + D2 = 0 для плоскости P2
Для нахождения пересечения плоскостей необходимо решить систему уравнений, состоящую из уравнений плоскостей P1 и P2. Пересечение может представлять собой прямую, плоскость или быть пустым множеством. Если пересечение является прямой, то количество общих точек будет зависеть от конкретного случая и расположения плоскостей.
Если система уравнений плоскостей P1 и P2 не имеет решений, то плоскости не имеют общих точек.
Пример:
Рассмотрим следующие две плоскости:
P1: x + y + z = 1
P2: 2x + 2y + 2z = 3
Для нахождения общих точек пересечения этих плоскостей решим систему уравнений:
x + y + z = 1 (P1)
2x + 2y + 2z = 3 (P2)
Поделим уравнение P2 на 2:
x + y + z = 1 (P1)
x + y + z = 1.5 (P2')
Уравнение P1 и P2' являются одинаковыми, поэтому система уравнений имеет бесконечное множество решений и соответствующие плоскости имеют бесконечное число общих точек.
Таким образом, геометрический способ позволяет определить количество общих точек у двух плоскостей, основываясь на их взаимном расположении в трехмерном пространстве.
Особые случаи подсчета общих точек плоскостей

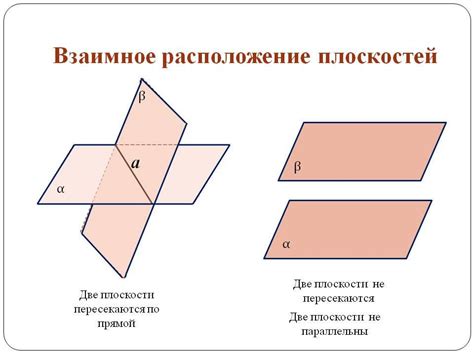
Один из особых случаев - когда две плоскости параллельны друг другу. В этом случае у них нет общих точек, так как они не пересекаются. Это может быть наглядно представлено двумя параллельными плоскостями на одной и той же высоте, которые ничем не пересекаются.
Еще один особый случай - когда две плоскости совпадают. В этом случае они имеют бесконечное количество общих точек, так как все точки одной плоскости также принадлежат другой. Это может быть наглядно представлено двумя идентичными прозрачными плоскостями, полностью накрывающими друг друга.
Также стоит отметить случаи, когда две плоскости пересекаются под определенным углом. В этом случае количество общих точек будет конечным и зависеть от радиуса плоскостей, разницы их углов и других параметров.
Все эти особенности нужно учитывать при подсчете общих точек плоскостей и выборе соответствующих методов для их определения.
Примеры решения задачи о подсчете общих точек плоскостей

Чтобы понять, сколько общих точек у двух разных плоскостей, необходимо рассмотреть их уравнения и сравнить их коэффициенты. В зависимости от значений этих коэффициентов, мы можем получить различные результаты:
| Случай | Описание | Количество общих точек |
|---|---|---|
| Параллельные плоскости | Если коэффициенты при одинаковых переменных совпадают, а свободные коэффициенты разные, то плоскости параллельны друг другу и не имеют общих точек. | Нет общих точек |
| Совпадающие плоскости | Если все коэффициенты при переменных совпадают, а свободные коэффициенты также совпадают, то плоскости совпадают и имеют бесконечное количество общих точек. | Бесконечное количество общих точек |
| Пересекающиеся плоскости | Если ни один из предыдущих случаев не выполняется, то плоскости пересекаются и имеют либо одну, либо бесконечное количество общих точек. | 1 или бесконечное количество общих точек |
Используя данные правила, можно определить количество общих точек у двух разных плоскостей, помимо этого метода существуют и другие способы решения этой задачи, включая геометрический исход и использование матриц и векторов.