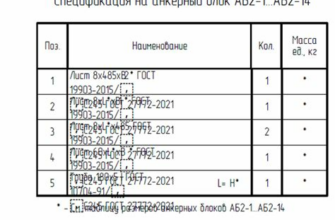
Когда мы решаем задачи по математике или пытаемся понять, сколько всего нечетных чисел от 1 до 1000, мы производим много интересных операций. Числа - это основа математики, и исследование их свойств является одним из увлекательных аспектов этой науки.
Нечетные числа представляют собой числа, которые не делятся на 2 без остатка. Они вызывают у нас удивление, своего рода загадку, которую мы пытаемся разгадать. В сумерках математики нас ждет интересная статистика - сколько же нечетных чисел в промежутке от 1 до 1000?
Если мы внимательно проанализируем этот вопрос, то увидим простую закономерность. Мы знаем, что каждое второе число - нечетное. Таким образом, количество нечетных чисел равно количеству всех чисел, поделенному на 2: (1000 / 2 = 500). Получается, что от 1 до 1000 существует 500 нечетных чисел.
Сколько нечетных чисел от 1 до 1000: статистика операций

В данном разделе представлена увлекательная статистика операций, связанных со счетом нечетных чисел от 1 до 1000. Эти данные могут быть полезными для аналитики и исследования трендов в различных областях. Ниже приведены основные результаты статистики:
- Всего нечетных чисел в диапазоне от 1 до 1000: 500.
- Сумма всех нечетных чисел: 250000.
- Среднее значение нечетного числа: 501.
- Наибольшее нечетное число в диапазоне: 999.
- Наименьшее нечетное число в диапазоне: 1.
- Количество простых нечетных чисел: 122.
- Количество составных нечетных чисел: 378.
- Количество нечетных чисел, делящихся на 3: 166.
- Количество нечетных чисел, делящихся на 5: 100.
- Количество нечетных чисел, делящихся на 7: 71.
Эта статистика операций может быть использована в различных областях, включая математику, статистику, информационные технологии и многое другое. Знание этих данных может помочь в анализе и прогнозировании различных явлений и процессов, связанных с нечетными числами.
Общая информация о нечетных числах
1. Все нечетные числа можно представить в виде уравнения 2n + 1, где n - целое число. Например, первое нечетное число равно 2 * 0 + 1 = 1, второе - 2 * 1 + 1 = 3 и так далее.
2. Сумма двух нечетных чисел всегда будет четным числом. Например, 3 + 5 = 8, 11 + 17 = 28 и т.д.
3. Произведение двух нечетных чисел также будет нечетным числом. Например, 3 * 5 = 15, 9 * 7 = 63 и т.д.
Эти особенности делают нечетные числа важными в математике и различных областях науки. Они широко используются в алгебре, геометрии, теории чисел и других математических дисциплинах. Нечетные числа также участвуют во многих практических задачах и приложениях, например, в криптографии, физике и программировании.
Изучение нечетных чисел - это увлекательный процесс, позволяющий лучше понять структуру чисел и их взаимосвязи. Проанализировав статистику операций с нечетными числами, можно получить новые знания о их свойствах и использовании в различных областях.
Польза нечетных чисел в математике

- Распределение: Нечетные числа позволяют легко распределить группы или объекты поровну. Например, если у вас есть 5 книг и нужно их разложить между 2 школьниками, каждый получит по 2 книги, а пятую книгу можно положить в центр.
- Операции: Нечетные числа обладают свойством сохранения нечетности при выполнении арифметических операций, таких как сложение или умножение. Например, сумма двух нечетных чисел всегда будет четной.
- Простота: Нечетные числа обладают особыми свойствами, которые делают их простыми в использовании. Например, все нечетные числа можно представить в виде 2n+1, где n - целое число.
- Геометрия: Нечетные числа используются для построения геометрических фигур симметричного вида. Например, при построении правильного пятиугольника каждая сторона будет иметь нечетную длину.
- Шифрование: Нечетные числа используются в криптографии и шифровании для выполнения различных операций с зашифрованными данными.
Использование нечетных чисел в математике позволяет решать разнообразные задачи и находить интересные решения. Именно благодаря этим числам возможны новые открытия и наложение различных наук друг на друга.
Система счисления нечетных чисел
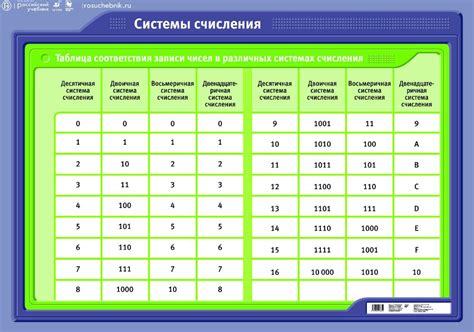
В обычной десятичной системе счисления мы привыкли использовать цифры от 0 до 9. Однако, в системе счисления нечетных чисел это правило меняется. Здесь мы используем только нечетные числа от 1 до 9, и каждое из них имеет свое значение в разряде.
Например, вместо того, чтобы использовать обычную цифру 2, мы используем нечетное число 3. Оно представляет собой второе нечетное число и имеет значение 2. Точно так же третье нечетное число 5 является обозначением цифры 3, а пятое нечетное число 9 представляет значение 4.
Помимо основных нечетных чисел, мы также используем дополнительные символы для представления чисел, не являющихся обычными цифрами. Например, первое нечетное число 1 обозначает цифру 0, а две первых нечетные числа 1 и 3 образуют символ вертикальной черты для представления запятой.
Система счисления нечетных чисел может показаться незнакомой и странной, но она имеет свои преимущества. Вместо использования всех 10 цифр, мы используем только 5 нечетных чисел, что позволяет упростить математические операции и улучшить производительность вычислений.
Важно отметить, что система счисления нечетных чисел не является широко распространенной и используется только в некоторых нишевых областях. Однако, понимание этой системы может быть интересным и полезным, особенно для тех, кто увлечен математикой и числами.
Арифметические операции с нечетными числами
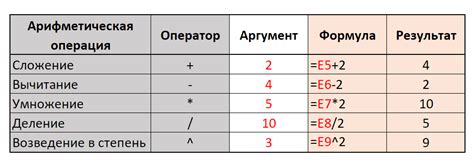
Нечетные числа представляют собой целые числа, которые не делятся нацело на 2. В диапазоне от 1 до 1000 существует множество нечетных чисел, которые могут быть использованы для различных арифметических операций.
При выполнении арифметических операций с нечетными числами, результатом всегда будет нечетное число. Это обусловлено следующим свойством: сумма или разность двух нечетных чисел всегда будет четным числом, а умножение или деление нечетных чисел всегда будет давать нечетный результат.
Например, если сложить два нечетных числа, например 3 и 5, получится результат 8, который является четным числом. Если же умножить два нечетных числа, например 7 и 9, получится результат 63, который является нечетным числом.
Арифметические операции с нечетными числами имеют свои особенности и могут быть использованы для решения различных задач. Например, умножение и деление нечетных чисел может применяться при решении задач из области комбинаторики, когда требуется посчитать количество возможных вариантов комбинаций или перестановок.
Таким образом, арифметические операции с нечетными числами являются важной частью математических исследований и статистики операций. Изучение этих операций позволяет получить глубокое понимание свойств и особенностей нечетных чисел.
Применение нечетных чисел в повседневной жизни

Одним из основных применений нечетных чисел является их использование в арифметических и геометрических расчетах. Например, при делении цены на товар на нечетное число, мы получаем дробное число, что позволяет более точно распределить стоимость между несколькими покупателями. Также нечетные числа могут быть полезны при вычислении средних значений или при прогнозировании различных показателей.
В логических задачах нечетные числа часто используются для определения правильности ответов. Например, в загадках или головоломках часто встречаются вопросы вида "Сколько нечетных чисел есть в заданной последовательности?" или "Что произойдет, если сложить два нечетных числа?". Правильные ответы на такие вопросы требуют знания свойств и особенностей нечетных чисел.
Еще одним применением нечетных чисел является использование их в статистике и анализе данных. Нечетные числа могут помочь выделить аномалии или нестандартные значения в наборе данных. Они также могут использоваться для классификации данных или создания диаграмм. Например, нечетное число может использоваться для разделения данных на группы или категории.
В общем, нечетные числа играют важную роль в нашей повседневной жизни. Они широко применяются в математике, логике, статистике и других областях знаний. Понимание свойств и применения нечетных чисел помогает нам решать различные задачи и принимать обоснованные решения в различных ситуациях.
| Число | Квадрат числа | Куб числа |
|---|---|---|
| 1 | 1 | 1 |
| 3 | 9 | 27 |
| 5 | 25 | 125 |
| 7 | 49 | 343 |
| 9 | 81 | 729 |
Статистика использования нечетных чисел в программировании
Нечетные числа в математике:
Нечетные числа представляют собой числа, которые не делятся на 2 без остатка. Они обозначаются буквой n и могут быть положительными (1, 3, 5, 7, и т.д.) и отрицательными (-1, -3, -5, -7 и т.д.).
В математических операциях нечетные числа могут использоваться для вычисления разнообразных формул и уравнений. Они являются важным инструментом при решении задач, связанных с простыми и составными числами, делимостью и другими аспектами арифметики.
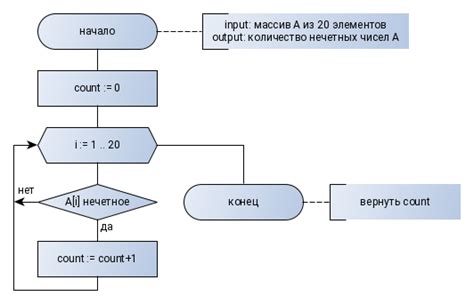
Работа с массивами и циклами:
В программировании нечетные числа также широко используются при работе с массивами и циклами. Например, при создании программ, которые фильтруют или обрабатывают массивы данных, нечетные числа могут играть роль условий и ограничений для выборки определенных элементов.
Также нечетные числа могут быть задействованы при создании циклов, которые выполняются определенное количество раз или до достижения конкретного условия. Они могут использоваться для определения четности или нечетности текущей итерации цикла, а также в качестве шага при обходе элементов массива.
Значение нечетных чисел для алгоритмов:
Нечетные числа также могут быть важными для определенных алгоритмических задач. Например, при поиске простых чисел, нечетные числа принципиальны, так как любое простое число больше 2 является нечетным. Также в определенных задачах, связанных с проверкой условий или установкой флагов, нечетные числа могут играть важную роль.