Углы являются одним из основных понятий геометрии, и поэтому их изучение играет важную роль в математике. Существует много различных типов углов, и каждый из них имеет свои характеристики и свойства.
Смежные углы - это углы, которые имеют общую сторону и общую вершину. Они расположены в одной плоскости и не пересекаются. Смежные углы могут быть как прямыми, так и острыми, в зависимости от их величины.
Прямой угол имеет величину 90 градусов и обозначается значком "∠". Он является наиболее известным и распространенным типом угла. Острый угол меньше 90 градусов и обычно представляет собой острый конус с "заточенными" вершинами.
Таким образом, смежные углы могут быть как прямыми, так и острыми. Например, смежные прямые углы могут образоваться при пересечении двух прямых, а смежные острые углы могут возникнуть при пересечении двух наклонных прямых.
Изучение и понимание смежных прямых и острых углов помогает нам анализировать геометрические фигуры и решать задачи, связанные с различными углами. Понимание их свойств помогает строить более точные измерения и предсказывать результаты различных геометрических операций.
Смежные прямые и острые углы: объяснение и примеры
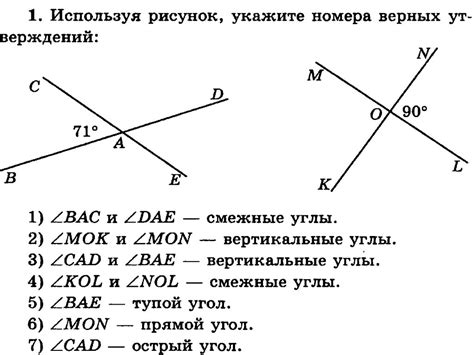
Может ли быть смежный прямой угол острый? Да, это возможно. Предположим, что у нас есть две прямые линии, которые пересекаются и образуют угол. Если этот угол меньше 90 градусов, то он будет острым. Поскольку эти две линии пересекаются только в одной точке, они являются также смежными прямыми.
Приведем пример. Возьмем две прямые линии AB и BC, которые пересекаются в точке B. Если угол ABC меньше 90 градусов, то он будет острым, а прямые AB и BC будут смежными.
| Пример: |
|---|
| |
В этом примере прямые AB и BC пересекаются в точке B, и угол ABC меньше 90 градусов, поэтому угол будет острым, а прямые будут смежными.
Таким образом, смежные прямые и острые углы могут сочетаться в геометрии.
Что такое смежные прямые?

Смежные прямые могут быть прямыми, наклонными, пересекающими или параллельными, главное условие - они должны иметь общую точку и образовывать угол. Например, линия A и линия B - смежные прямые, потому что они имеют общую точку и образуют угол.
Смежные прямые часто встречаются в геометрии и используются для определения свойств углов, плоскостей и фигур. Изучение смежных прямых помогает лучше понять и описать геометрические формы и их взаимосвязи.
Что такое острые углы?

Острые углы широко встречаются в различных областях науки и повседневной жизни. Например, в геометрии, острые углы играют важную роль при изучении треугольников, квадратов и других фигур. Они также используются в архитектуре и дизайне для создания эстетически приятных и сбалансированных форм и углов.
Одним из примеров острых углов является треугольник, где все его углы меньше 90 градусов. Также острые углы присутствуют во многих ежедневных объектах. Например, острые углы можно наблюдать в форме лезвия ножа, угла склона склона крыши дома или угла наклона параболической антенны.
Острые углы имеют свои специальные свойства и исследования, которые помогают в понимании различных аспектов геометрии, физики, архитектуры и других наук. Они также могут использоваться для решения различных задач и проблем в реальном мире.
Могут ли быть смежные прямые и острые углы?

Один из таких случаев - это ситуация, когда смежные прямые линии образуют острый угол с третьей прямой линией. Например, рассмотрим треугольник ABC, где AB и BC - смежные прямые, а AC - третья прямая. Если угол BAC острый, то прямые AB и BC будут смежными прямыми, образующими острый угол с третьей прямой AC.
Еще один пример - это ситуация, когда две смежные прямые линии образуют острый угол с одной и той же прямой линией. Например, рассмотрим две смежные прямые линии AB и BC, которые образуют острый угол с прямой линией AD. В этом случае, точка B будет общей для двух смежных прямых AB и BC и будет являться вершиной острого угла.
Таким образом, хотя на первый взгляд кажется, что смежные прямые и острые углы не сочетаются, на самом деле они могут встречаться в геометрических фигурах и образовывать интересные комбинации. Это демонстрирует разнообразие и гибкость геометрии.