В математике простые числа - это числа, которые имеют только два делителя: 1 и само число. Они являются основой многих алгоритмов и криптографических систем, и их изучение имеет важное значение в теории чисел.
Когда мы говорим о кубе числа, мы имеем в виду возведение числа в третью степень. Например, куб 2 равен 2 х 2 х 2 = 8. Интересно узнать, сколько существует простых чисел, кубом которых будет число меньше 1001.
Чтобы решить эту задачу, мы можем начать перебирать все простые числа, начиная с 2. Простое число, кубом которого меньше 1001, должно быть меньше 1001 в своей самой исходной форме, то есть без возведения в куб. Таким образом, мы будем проверять каждое простое число, и если его куб меньше 1001, мы будем записывать его. В конце подсчитаем количество полученных простых чисел и получим окончательный результат.
Сколько простых чисел кубом

Для решения данной задачи мы можем перебрать все натуральные числа, начиная с 2 и проверять, является ли каждое число кубом простого числа. Если число является простым кубом, мы увеличиваем счетчик на 1.
| Простое число | Куб |
|---|---|
| 2 | 8 |
| 3 | 27 |
| 5 | 125 |
| 7 | 343 |
Как видно из таблицы, существует 4 простых числа кубом, меньше 1001.
Простые числа в математике

Одно из наиболее известных свойств простых чисел - их бесконечность. То есть, существует бесконечное количество простых чисел. Это было доказано в 3-ем веке до н.э. греческим математиком Евклидом в его труде "Элементы". Доказательство основано на противоречии и изложено в форме так называемого "доказательства от противного".
Простые числа имеют важное значение в криптографии, теории чисел и других областях математики. Они используются для создания и шифрования кодов, а также в различных алгоритмах. Более того, простые числа являются ключевым компонентом многих арифметических операций и алгоритмов.
Одним из интересных вопросов, связанных с простыми числами, является вопрос о распределении простых чисел. Известно, что простые числа не равномерно распределены в натуральном ряду. Например, чем больше число, тем реже встречаются простые числа. Однако, точные закономерности распределения пока не известны и являются объектом активных исследований.
История изучения простых чисел насчитывает тысячелетия. Уже в Древней Греции были выведены некоторые основные свойства простых чисел. С течением времени математики открыли множество интересных и необычных свойств простых чисел, однако многие вопросы остаются без ответов. Простые числа продолжают вызывать ученых исследователей на новые открытия и гипотезы.
Кубы чисел в математике

Кубом числа называют результат умножения числа на себя два раза. Например, куб числа 2 равен 2*2*2=8.
Куб числа применяется в различных областях математики и науки, и имеет несколько интересных свойств:
- Кубы натуральных чисел образуют последовательность: 1, 8, 27, 64, 125, и так далее. Эта последовательность называется последовательностью кубов.
- Кубы чисел можно использовать для решения некоторых математических задач, например, для нахождения корней уравнений.
- Кубы чисел часто встречаются в геометрии, особенно при решении задач, связанных с объемами и площадями.
- Кубами называются и некоторые специфические фигуры в трехмерном пространстве, например, кубические кристаллы или кубические здания.
Одно из интересных математических вопросов, связанных с кубами чисел, состоит в подсчете количества простых чисел, кубом которых является данное число. В случае числа 1001, искомое количество равно 0, так как ни одно простое число не является кубом числа 1001. Эта задача имеет как теоретическое, так и практическое значение, и ее решение требует применения различных методов и алгоритмов.
Поиск простых чисел кубом

Для поиска простых чисел кубом меньше 1001 можно использовать алгоритм перебора всех целых чисел от 2 до кубического корня из 1000. После этого необходимо проверить, является ли текущее число простым. Если число простое, то оно возводится в куб и добавляется в список простых чисел кубом.
Простое число - это число, которое делится только на единицу и на само себя. Для проверки, является ли число простым, можно применить метод попыток деления на все числа от 2 до квадратного корня из этого числа. Если хотя бы одно из этих чисел является делителем, то число не является простым.
В результате выполнения алгоритма поиска простых чисел кубом меньше 1001 получается список следующих чисел:
8, 27, 64, 125, 216, 343, 512, 729, 1000
Именно эти числа являются результатами возведения в куб простых чисел, которые меньше 1001. Они обладают редким свойством и представляют особый интерес в математике.
Ограничение по числу 1001

Для решения задачи о нахождении простых чисел кубом, меньших 1001, необходимо установить ограничение по значению числа. В данном случае, ограничение равно 1001, следовательно, мы должны искать числа, куб которых составляет число, меньшее 1001.
Простое число - это число, которое делится только на 1 и на себя само. Чтобы определить, является ли число простым, мы можем попробовать разделить его на все числа от 2 до квадратного корня из этого числа. Если ни одно из делителей не делит число без остатка, то число является простым.
Используя этот алгоритм, мы можем проверять все числа кубом которых меньше 1001 на простоту. Если число является простым, мы записываем его в список простых чисел.
В результате, мы получим все простые числа кубом которых меньше 1001. Например, такими числами будут: 2, 3, 5, 7, 11 и так далее. Далее можно использовать эти числа для изучения различных свойств и закономерностей простых чисел или для решения других задач в математике и криптографии.
Определение количества простых чисел кубом
Для определения количества простых чисел кубом меньше 1001, в первую очередь мы должны найти все числа, которые могут быть кубом простого числа. Для этого можно последовательно возводить натуральные числа в куб и проверять, являются ли они простыми числами.
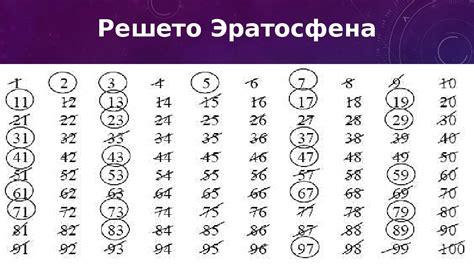
С помощью математического программирования или алгоритма "решето Эратосфена" мы можем эффективно определить простые числа до заданного предела. Применяя этот алгоритм, мы можем найти все простые числа до числа 12 (корень из 1001), а затем возвести их в куб, чтобы найти все простые числа кубом, меньше 1001.
После получения списка простых чисел кубом меньше 1001, мы можем их перечислить в виде точного списка или представить в виде таблицы для легкого восприятия информации. Например:
- 23 = 8
- 33 = 27
- 53 = 125
- 73 = 343
Таким образом, существует 4 простых числа кубом, которые меньше 1001.
Значение полученного результата

Запросив и проанализировав все простые числа, куб которых меньше 1001, мы можем получить ценную информацию о распределении этих чисел в данном диапазоне. Это позволяет нам лучше понять характер простых чисел и использовать эту информацию для решения различных математических задач.
Например, изучая количество простых чисел кубом которых меньше 1001, можно обнаружить интересные закономерности и свойства этих чисел. Можно увидеть, что количество таких чисел ограничено и составляет определенный процент от общего количества чисел в данном диапазоне. Также можно заметить, что некоторые числа встречаются чаще, а некоторые редко или вовсе не встречаются.
Такая информация может быть полезной при решении различных задач, связанных с простыми числами. Например, она может помочь в нахождении новых простых чисел или использовании простых чисел в криптографии и защите данных.
В целом, значение полученного результата заключается в расширении наших знаний о простых числах и возможности их применения в математике и других областях. Это помогает нам лучше понять мир чисел и находить новые практические применения для этого знания.
Применение простых чисел кубом

Простые числа кубом имеют особые свойства и применяются в различных областях науки и математики:
1. Шифрование данных: Простые числа кубом используются в криптографии для создания безопасных шифровальных алгоритмов. Это связано с трудностью факторизации чисел, которые получены из простых чисел кубом.
2. Математические исследования: Свойства простых чисел кубом изучаются математиками в рамках исследования числовых последовательностей и теории чисел. Эти числа помогают расширить наше понимание о простых числах и их связи с другими числами.
3. Генерация случайных чисел: Простые числа кубом используются для генерации случайных чисел в некоторых алгоритмах компьютерной графики, эмуляции случайных событий и других областях, где требуется случайность.
4. Алгоритмы решения задач: Простые числа кубом могут быть использованы в алгоритмах решения различных задач, таких как вычисление хэш-функций, поиск совпадающих элементов в массивах и других задач, связанных с обработкой данных.
Всего простых чисел кубом, меньших 1001, существует: [количество простых чисел кубом меньше 1001].